第１８回助教の会

第１８回目の助教の会では，数理第５研究室の鈴木大慈さんに発表していただきました．発表のタイトルは”PAC-Bayesian Bound for Gaussian Process Regression and Multiple Kernel Additive Model”というもので，無理やり和訳すると「ガウス過程回帰を用いたマルチプルカーネル加法モデルに対するPAC-Bayesian 上界」とでも言うのでしょうか．本発表はConference on Learning Theory (COLT2012) という学習理論の国際会議での発表を，一般の数理の人向けに少しアレンジしたものでした．

発表タイトルの意味するところを読み解いていくと，研究成果としては，ノンパラメトリック回帰のためのスパース加法モデルを推定するために用いられるマルチプルカーネル学習に対し，PAC-Bayes 的な手法を用いて収束のレートを評価したというものです．その際，事前分布にガウス過程を導入し，これが理論評価のための１つのキーになっているそうです．

少し用語の説明も加味しながら研究成果をざっくりと解説すると，まずノンパラメトリック回帰とは，学部の授業で習う線形回帰Y=Xθのようなパラメータθを含む形をとらずに，（ある程度なめらかな関数を用いて）モデルを推定する方法です．やりたいのは，下図のように，サンプル点が与えられたときに適切な曲線をえがくことです．

スパース加法モデルは高次元ノンパラメトリック回帰において各説明変数ごとに（非線形）関数を割り当て，それらの和をデータに当てはめるモデルです．その際，各非線形関数を再生核ヒルベルト空間というある関数空間から適当にとってきた関数で表現する，いわゆるマルチプルカーネルが有用であるということでした．具体的にモデルを推定する方法としては，ある最適化問題を解くことになりますが，その際，正則化項を導入して少ないカーネル関数の和でモデルを表現することを目指します．これがマルチプルカーネル学習です（下図）．

この推定において，サンプル数nを増やすにつれて推定された関数は求めるべき関数に収束します．その収束性に関しては，Restricted Eigenvalue 条件を仮定することで高速なレートを達成できることが理論保証されていましたが，Restricted Eigenvalue 条件は強い仮定で，これを外すことが望まれていました．

鈴木さんはこの問題に対し，上に示した意味でのスパースな解による推定と，事前分布に（スケーリングした）ガウス過程のミクスチャーを導入した，ベイズ的マルチプルカーネル学習を考え，このタイプのマルチプルカーネル学習を行えば，既存の収束レート評価に必要だったRestricted Eigenvalue 条件を外した形で高速な収束レートを実現できることを示しました．発表ではいくつかの問題例に対する収束レートを示し，スケールミクスチャーの導入により高速なレートの評価ができることを強調してらっしゃいました．

鈴木さんの助教の会での発表は２回目でして，今回は数式や関数解析に登場する用語がかなり多くて専門的な内容になっているなあと思って１回目の鈴木さんの発表（第１回助教の会）のブログを見てみると，前回もかなり内容が盛りだくさんだったことを思い出しました．鈴木さんの手を抜かない性格と研究の迫力を感じさせられました．

数理3研助教 相島健助

PAC-Bayesian Bound for Gaussian Process Regression and Multiple Kernel Additive Model from Taiji Suzuki

第17回助教の会

今年度5回目となる今回はお隣りのシステム情報学専攻から亀岡弘和先生をゲストとしてお招きして「スパース表現による音響信号処理」というタイトルでお話しいただきました。亀岡先生は2007年に博士の学位を取られてからNTTコミュニケーション科学基礎研究所に勤めていらっしゃいますが、2011年からは客員准教授として6号館に戻っていらっしゃいます。

今回は複素NMFと、複合自己回帰系という2つの手法に基づいた音源分離の話を紹介して頂きました。音源分離はその名前の通り、観測された音声・音響信号を少ない数の音源に分離する技術で、音楽の録音を楽器の音色ごとに分離したり、会議の録音を話者ごとに分離したりするなど様々な応用があります。

NMF (Nonnegative Matrix Factorization; 非負行列分解）は音源分離に頻繁に用いられる手法で、数学的には与えられた非負の要素からなる行列（非負行列）を2つの非負行列の積に分解するというふうに定式化されます。そもそもどうして非負の要素からなる行列を考えるかと言うと、音響信号のフーリエ変換の振幅は負の値を取らないからです。実際の音声信号の振幅スペクトログラムを図１右上に示します。振幅スペクトログラムは縦の長さがフーリエ変換の周波数の数、横の長さが音響信号の長さ（時間）の非負行列です。この図からわかるように、現実の音声信号は異なる周波数の音がばらばらに鳴っているのではなく、かなり規則的にそろって発生しています。このことから、「どの周波数の信号をどれだけ含んでいるか」という情報と「どのタイミングで音が鳴ったか」という情報のペアをひとつの音源とみなし、現実の音声信号を複数の音源の重ね合わせとして表現しようというのが、NMFを用いる動機です。多くの既存研究では振幅スペクトログラムに対してNMFを適用しています（図１右上）。NMFでは前者の「それぞれの音源はどの周波数の信号をどれだけ含んでいるか」という情報を行列Hで、後者の「それぞれの音源はどのタイミングでどの強さで鳴るか」という情報を行列Uで表現します（図１右下）。

図1 振幅スペクトグラムの分解表現

既存のNMFは振幅スペクトログラムを対象としているため、観測信号が複数の音源が線形に混ざったものであったとしても、振幅スペクトルの上では線形な混合にならないという問題点がありました。亀岡先生はこの点に注目し、混合の線形性が成り立つ複素スペクトルの上でNMFを定式化することに成功しました[1]。振幅スペクトルの代わりに複素スペクトルを対象にするためには信号の位相を考える必要があります。複素NMFは上述のペアがすべての時間点、周波数において位相の任意性を持っていると考え、これを含めて最適な信号の分解を計算するアルゴリズムになっています。複素NMFでは位相の情報も最適化の中で陽に扱っているので、従来の振幅スペクトログラムに基づくNMFの場合のように後処理で位相を求める必要がありません。

このアルゴリズムを使うと分解した1つ1つの音声信号の成分に対して、音量をコントロールしたりピッチを変更したりすることができます。これらは亀岡先生が作成された MusicFactorizer というツールのデモページで聞くことができます。

後半のお話は、複数の人間が同時に話しているような状況での（複数のマイクの）録音から個々の話者の音声を分離する、いわゆるカクテルパーティー問題が対象です。

ここでの音源とは人間の発する音声ですので、どのような周波数でも好きに組み合わせられるわけではありません。このような音声をモデル化するための有名な手法のひとつとして「自己回帰系」があります。P次の自己回帰系は、白色雑音を入力として、過去P次点前までの出力に依存して現在の出力が決まるような、時系列モデルです。従来の自己回帰系では、入力が白色雑音に限定されているため、P個の自己回帰フィルタ係数で音源の周波数特性を表現する必要がありました。一方、亀岡先生の提案している「複合自己回帰系」モデルは複数の白色とは限らないパワースペクトル密度と、複数の自己回帰フィルタを用意し、その組み合わせで音源を表現します。つまり、あらかじめ多くのパワースペクトル密度と多くの自己回帰フィルタを用意しておけばその組み合わせで各フレームの音源を簡単に表現することができるというわけです。その上、従来はフレームと呼ばれる信号の単位ごとに自己回帰フィルタを計算していたのですが、「複合自己回帰系」では用意しておくパワースペクトル密度や自己回帰フィルタを信号全体で最適化し、フレームをまたいで再利用することができるので無駄がない、というメリットもあります。

図2: 複合自己回帰系

このような信号源のモデルに残響のモデルを組み合わせることにより、現実的な環境で従来の方法よりうまく話者を分離できることが分かりました[2]。音声信号処理の伝統的な方法である自己回帰モデルと、少ない数の基底を組みあせて使うという行列分解モデルの考え方がうまく組み合わさって高い性能を出せるという点が非常に興味深いと感じました。

数理6研助教　冨岡亮太

Kameoka2012 talk07 1 from kame_hirokazu

[1] 亀岡弘和, 小野順貴, 柏野邦夫, 嵯峨山茂樹 (2008) 複素NMF： 新しいスパース信号分解表現と基底系学習アルゴリズム. 日本音響学会論文集.
[2] 濱村真理子, 亀岡弘和, 吉岡拓也, ルルージョナトン, 柏野邦夫 (2010) 複合自己回帰系による音声パワースペクトル密度モデルを用いたブラインド音源分離と残響除去. 日本音響学会講演論文集.

第１６回助教の回

第１６回目となる今回の数理助教の会は, 数理第４研究室の西遼佑さんに「個々の車の振る舞いによる合流渋滞の改善手法の研究」について発表していただきました。西さんは、日本の渋滞研究で有名な西成先生の研究室で学位を取得後、特任研究員として数理４研で研究活動を進めています。

日本で交通渋滞は、１年で１１兆円もの経済損失につながっているとの試算があるそうです。そのため、渋滞緩和は重要な社会的課題の一つとなっています。 渋滞緩和では、道路などのインフラ整備（大規模）、信号やスピード制限などの規制を設ける方法、そして、個々の車の振る舞い（例：車間距離）に注目するという３つの切り口があります。インフラ整備や交通規制は大掛かりになりますので、個々の車の動きに注目した、低コストで渋滞緩和に効果を発揮する方法が望まれています。高速道路上でインターチェンジや合流部はゆるやかな上り坂（サグ部）、トンネルについで、渋滞の発生する場所ですが、日本で特に有名なのは小菅ジャンクション(JCT)だそうです。

交通流の研究は意外に歴史が古く、１９３０年代（日本は昭和初期）のアメリカで既に様々なデータ(速度 - 車間距離など)がとられていたようです。１９９０年代になると、物理学的な手法の１つとして、一つ一つの車を自己駆動粒子(Self Driven Particle; SDP)とみなし、交通流を多数の自己駆動粒子の集まりととらえて数理モデルで表現する研究が発展しました。また、統計物理の立場で、渋滞している状態と、そうでない状態を相転移ととらえるような研究もあるそうです。

西さんは、上のような渋滞現象の数理モデルでの記述から、さらに一歩進んで、実際に渋滞が起きるケースに注目し、渋滞緩和の具体的な方法を研究しています。私はこの点が非常に優れていると思いました。それでは、西さんたちが注目している小菅ジャンクション（JC）での渋滞緩和のアイディアをみていきましょう。

一般に車線変更が起きるような道路ではジッパー配置が理想的とされています。ジッパー配置とは、互い違いなど隣り合わずに並走している状態で、いったんジッパー配置になればスムーズに車線変更が可能となります。

ところが、下図のような、二つの道路がいったん合流して、すぐに分岐するような場所（例：小菅JCT）では、ジッパー配置になる前に車線変更してくる車は、後ろの車を減速させて、渋滞を発生させてしまいます。そこで、小菅JCTのような合流地点で、図の下側にあるようなオレンジライン（車線変更禁止ライン）を引くことを考えます。合流直後の車線変更を防ぎ、車線間相互作用を活用してジッパー配置を励起するのが狙いです。非常に安価であるというメリットがあります。

図の下側のように、オレンジラインに沿って上下車線の車がジッパー配置になることでスムーズに車線変更がおきます。 さて、このジッパー合流ですが、小菅JCTのように、合流部分が７～８００メートルと短い区間では、オレンジラインの長さの調整が大変難しいそうです。また、実際に実験するのも大変コストがかかり危険を伴うため、まずは、数値シミュレーションで解析する必要があります。 西さんは、セルオートマータ(CA)を用いて、２車線の系で自動車がどのようにふるまうかを様々な条件のもと、シミュレーションしています。

 各車は、隣の車線に車があると減速したり、前が空いたら加速するといった複雑なふるまいをしますので、連続時間で表現するのは難しく、まずは、離散的な時間で１マスずつ車を動かしています。上のモデルでは、パラメータ a  (0<a<1) を動かした時にどれだけ短い距離でジッパー配置を達成できるかがわかりました。また、平均場近似による計算でも説明できます。他にもパラメータを調整して様々な結果がわかってきました。しかしながら、このようなシンプルな数理モデルでも、実際の状況に合うパラメータをどうやって推定すればいいかわからないという状況で、応用には様々な課題があるそうです。
私の感想としては、まず、実験的に検証しづらい現象をここまで数学的にモデル化できたというのが驚きです。 これは、他に先行研究のない全く新しい研究で、今後、日本が世界をリードできる分野の一つと感じました。また、１％でも渋滞緩和ができれば、経済効果としては単純計算で１年１０００億円になります。道路での実証実験と実用化を目指し、数理モデルでのシミュレーションにある程度の予算と人材を投入すべきと思います。
発表では、既にある小菅JCTの課題をとらえて解決案を探っていましたが、今後の道路網整備や都市計画などへも、非常に有効な知見を与えられるのではないでしょうか。道路のような巨大なインフラでは、ちょっとした設計ミスが将来、多額の国家損失になりえますので、やはり、ある程度の研究予算を投入すべきと思いました。

Sj kseminar ryosukenishi_for_slideshare

View more presentations from sgocvianfwefvdsd0129vnalc

数理４研　田中冬彦

第15回助教の会

第15回助教の会では公立はこだて未来大学の田中健一郎さんに発表していただきました．田中さんは2007年3月に東京大学大学院情報理工学系研究科数理情報学専攻にて博士号を取得後，東京海上日動火災保険株式会社に就職．2011年4月より公立はこだて未来大学システム情報科学部複雑系知能学科の助教として研究活動をされています．大学院時代の同期である数理4研助教の田中冬彦さんの仲介により今回の発表が実現しました．発表タイトルは「微分作用素に対するHillの方法の収束次数および明示的な誤差上界」ということで，微分方程式に対する数値解法であるスペクトル法，特にHillの方法に関する研究成果のお話でした．

物理的な現象や社会的な現象の中には微分方程式により記述されるものが多くあります．本発表で出てくる波の挙動はその代表的な例といえます．微分方程式の数値解法としてはスペクトル法の他に差分法や有限要素法がよく知られています．スペクトル法の特徴は，他の手法と比べて非常に精度よく解を近似できることです．田中さんの研究は，Hillの方法による近似誤差の収束次数と上界に関する理論的な結果を与えています．特に，誤差上界の評価については，スペクトルの真値を利用しないことで計算可能な上界が得られています．数値手法を実際に利用する上で理論的な評価は重要な指針となります．本発表の主結果（の一部）は次の通りです．

図１：主結果

具体的な問題設定は以下の通りです（図２）．まず，対象は非線形波動方程式です．この非線形波動方程式を定常解の周りで線形近似することにより，摂動$\eta$を使って解$\zeta$の安定性を調べることが目的です．ここではさらに$\eta(x,t)=\Psi(x)\exp(\lambda t)$を仮定して，時刻に依存しない関数$\Psi$の微分方程式へと変形します．今，解の安定性は微分作用素$S_p$のスペクトル，特にその実数部分の正負で判定されます．つまり，スペクトルの実部が負であれば安定，正であれば安定ではないということです．以上より，問題は微分方程式$S_p\Psi = \lambda \Psi$を数値的に解くことに帰着し，あとはこの微分方程式を数値的に解けばよいことになります．そして田中さんは，Hillの方法による近似を考え，その収束次数と誤差上界を理論的に導出しています．

図２：非線形方程式の変形

Hillの方法はもともと1886年にHillにより提唱されましたが，有効な数値計算手法として認識されたのはごく最近になってからの話だそうです．Hillの方法による近似は
1. Floquet-Bloch分解
2. Fourier級数による近似
の２段階で行われます．まず，Floquet-Bloch分解の概要を図３に示します．Floquet-Bloch分解をなぜ行うかというと，それは作用素$S_p$が連続スペクトルをもち直接的な解析が難しいためです．Floquet-Bloch分解では，非周期性を指定するパラメータ$\mu$の値に応じて周期解と微分作用素$S_p^{\mu}$を考えます．パラメータ$\mu$の値を変化させることで作用素$S_p$のスペクトルがすべて現れ，$\mu$の値ごとに作用素$S_p^{\mu}$が点スペクトルだけをもつので解析がしやすくなります（図４）．

図３：Floquet-Bloch分解（その１）

図４：Floquet-Bloch分解（その２）

Fourier級数による近似では，周期関数を使って周期解を無限級数展開し，$2N+1$項の有限打ち切りによる近似を行います（図５）．Hillの方法により，微分方程式$S_p\Psi = \lambda \Psi$という問題がパラメータ$\mu$ごとに$2N+1$次正方行列の固有値問題に帰着されます．

図５：Fourier級数による近似

固有値問題の解ともとの問題$S_p\Psi = \lambda \Psi$のスペクトルとの誤差を評価するために，田中さんは誤差を「固有値問題の固有関数ともとの問題の固有関数との誤差」と「Fourier近似による誤差」の２つに分解しました（図６）．後者についてはFourier解析の一般論から誤差の評価が得られます．前者の評価にはGershgorinの定理とDunford積分という２つの道具が使われています．Gershgorinの定理は固有値の存在する範囲を教える定理であり，Dunford積分は複素解析における留数の定理を作用素に対して考えたようなものとのことです．上界の評価においては，収束次数の評価で用いた手法に工夫を加え，スペクトルの真値を直接利用しないことで明示的な上界を与えています．以上より精度誤差の収束次数と上界に関する主結果を得ます．

図６：精度誤差評価のためのアイデア

例題について，近似誤差と田中さんの与えた上界との比較結果も紹介されました（図７）．

図７：精度誤差と上界との比較

今回の田中さんの発表では「実際に計算できるもので評価する」という点が強調されていたように思います．誤差の理論的な評価は数値手法に関する重要な指標です．特に，実際に計算して使える指標の存在はやはり心強いものだと思います．大変興味深く面白いお話でした．


数理5研助教 廣瀬善大

Jyokyo-kai-20120605

View more presentations from ketanaka

第14回助教の会

今年度より助教の会に入会した林です．5月28日に行われた第14回助教の会では廣瀬善大さんに "Dimension Reduction Based on the Geometry of Dually Flat Spaces" （双対平坦空間の幾何学に基づいた次元削減）というタイトルで発表していただきました．

廣瀬さんは昨年度３月に東京大学の数理５研で博士号を取得され，今年度より同研究室で助教に着任されました．

今回のお話は廣瀬さんの博士課程での研究成果をまとめたもので，一言でいうと Least Angle Regression (LARS, 最小角回帰法) の幾何学的な拡張と具体的な確率モデルへの応用について発表されました．発表の前半ではLARSの解説とその拡張について，後半ではグラフィカルガウシアンモデルへの応用が紹介されています．

そもそものモチベーションとして，統計モデルを学習させるときに疎（スパース）な解を得たいというものがあります．例えば，線形回帰の問題では入力Xと出力yの組に対して線形な関係を仮定し，二乗誤差が最小となるような重みパラメータを求めます（最尤推定）．この求められた重みの強さによってどの特徴量がyの予測に役立っているかを知ることができますが，重みが疎，すなわち多くの値が0で埋まっていればyと関係する特徴量を簡単に絞り込むことができます．一般的に線形回帰で求められた解は疎にならないため，L1ノルムによる正則化項を付け加える（LASSO）などなんらかの工夫が必要となります．

LARSは線形回帰の解を疎に求めるアルゴリズムとして2004年に提案されました．

• Efron, Hastie, Johnstone and Tibshirani: Least Angle Regression (with discussion). Annals of Statistics, vol. 32 (2004), pp. 407-499.

LARSによるパラメータ推定の手順は一種の繰り返しアルゴリズムになっています．通常の最尤推定値を$\bar{y}$としたとき，LARSは予測に使う特徴量を一つづつモデルに加えていき，原点から$\bar{y}$にいたるまでのパスを計算します．具体的なアルゴリズムは以下になります．またアルゴリズムの具体例を図１に示します．

1. すべての特徴量を使わない状況，すなわちすべての重みを0としてスタート．
2. まだ使っていない特徴量のうち，相関が一番大きい特徴量を基底に加える．
3. 基底に入っている特徴量と$\bar{y}-\hat{\mu}$との相関を考える．$\hat{\mu}$がその上を動くような直線として，これらの相関が互いに等しいままであるような直線をとる（角の二等分線に相当する直線）．使っていない特徴量のうち，これらの相関と同じだけ大きい相関をもつ特徴量が現れたら，2.に移る．
4. 推定値$\hat{\mu}$が$\bar{y}$に到達するまで2.と3.を繰り返す．

このアルゴリズムをk回目で止めるとk個の非ゼロな重みをもつパラメータを得ることができるため，ユーザは任意の疎な解を得ることができます．

図１：LARSによって得られるパス（赤線）

廣瀬さんはLARSのアイデアを情報幾何の世界で解釈しなおし，他の統計モデルにとって自然な拡張を行いました．LARSはパスを求める際，角の二等分線というユークリッド幾何的な性質を用いており，この性質は線形回帰と相性がいいものですが，一般の統計モデルにとってはそうとは限らないからです．LARSは角度という幾何的性質を用いたアルゴリズムですが，廣瀬さんはこの代わりに距離を用いてLARSの拡張を行いました．具体的にはKL擬距離という確率分布にとって自然な距離を導入し，一般化線形モデルやグラフィカルガウシアンモデル(GGM)に応用されました．（この記事では深くは立ち入りませんが，情報幾何とはユークリッド幾何を一般化したもので，ある確率分布がある一点として表現されるような空間を扱う学術体系です．）

発表の後半ではGGMへの応用が紹介されました．GGMは複数の変数が与えられたとき，ある２変数の間に（他の変数が与えられた下での）条件付き独立性があるかないかを調べるときに用いられるモデルです．具体的にはすべての変数は１つの多次元ガウス分布から生成されたと仮定し，推定された精度行列（共分散行列の逆行列）が0であれば対応する変数間には条件付き独立性がないと考えます．変数の数が増えるにしたがってその組み合わせの数も増加するため，ここでもやはり疎な解が歓迎されます．

図２：提案手法の実験結果

実データを用いた実験もいくつか紹介されました．その１つは学生８８人の数学５科目の成績から科目間の条件付き独立性を調べたもので，図２は実際に提案手法によって得られた結果を示しています．２科目間の条件付き独立性の有無がグラフ上の辺によって表現されており，たとえば代数と解析の従属性が強いとされるなど興味深い結果となっています．シミュレーションでは提案手法が既存手法よりも優れた予測精度を達成したことが示されています．

今回の廣瀬さんのお話は，線形回帰モデルにのみ用いられてきたLARSアルゴリズムを一般の統計モデルに対しても使えるよう拡張されたという点で，非常に意義深いと感じました．自分も含め，最近は確率モデルや統計モデルを用いた研究はとても一般的になってきたため，ユーザの立場からもこのような一般化はありがたいのではないでしょうか．ただ，提案手法の計算量はそこそこかかってしまう（GGMの場合，変数の数の二乗のオーダ）と伺ったので，今後は計算の効率化にぜひ期待させていただきたいと思いました．

jokyo20120528

View more presentations from YoshihiroHIROSE

数理第6研究室　林浩平

第13回助教の会

新年度第1回の助教の会は数理6研の林浩平さんに「Generalization of Tensor Factorization and Applications」というタイトルで話して頂きました。林さんは3月に奈良先端科学技術大学院大学情報科学研究科で博士号を取得し、4月から日本学術振興会特別研究員として数理6研に所属しています。

林さんは博士課程の間からデータマイニングにおけるテンソル分解 (Tensor Decomposition) と呼ばれる手法を研究しています。今回は二つの話題を紹介していただきました。前半はノイズにガウス分布を仮定しない多種多様な要素を持つテンソルに対するテンソル分解、後半はテンソルに低ランク性を仮定しないテンソル分解です。

前半のお話は、一昨年の国際会議ICDM2010で発表[1]された、多種多様な（ヘテロな）要素を持つテンソルに対するテンソル分解です。

図1: ユーザ × 商品  × 時間の3階テンソルとして表現された購買データ

そもそもテンソルというのはテーブル形式のデータを多次元に拡張したもので、例えば、複数のユーザがいくつかの種類の商品をある時刻に購入したという購買データを考えるとユーザ × 商品  × 時間の3階テンソルとして表現することができます（図１）。あるいは、商品の代わりにユーザを複数種類のセンサーが取り巻いているユビキタスコンピューティング的状況を考えると、センサーデータはやはりユーザ  × センサー  × 時間の3階テンソルとして表現されます。テンソル分解はこのようなデータを低次元の因子行列の積で近似（低ランク近似）することでデータを見やすくしたり、見えていない要素を予測したりするための方法です。

ここでなぜ、データのヘテロ性が問題になるかと言うと、例えば購買データであれば数量、センサーデータではセンサーの種類によって、電子メールの件数などの非負整数値を取るセンサー、位置情報などの実数値を取るセンサーなどがあるからです。このように要素によって異なる種類の値を取るテンソルを近似するための基準はどのように選んだらよいのでしょうか。

図2: 指数型分布の例（ガウス分布、ポアソン分布、ベルヌーイ分布）

この問題に対して、林さんは指数型分布族（図2）に基づく確率モデルを用いて確率モデルの対数尤度を近似の基準として用いることを提案しています。林さんの方法では指数型分布族と対数尤度を用いることで異なる種類の要素を自然に扱うことができます。例えば実数を取る要素であればガウス分布、非負整数値を取る要素であれば分布を使うことができます。指数型分布族は非常に広いクラスの確率分布をカバーする確率分布のファミリーで、図2に示すように関数Ψの選び方で様々な分布を表現することができます。林さんの研究ではD個の観測値の要素ごとに互いに異なる関数Ψを用いて、対数尤度に正則化項を加えたもの
\[ \mathcal{L} =\sum_{d=1}^{D}\left(x_d\mathbf{w}_d^\top\mathbf{z}-\psi_{h_d}(\mathbf{w}_d^\top\mathbf{z})\right)-\frac{1}{2}\|\mathbf{z}\|^2-\sum_{m=1}^{M}\frac{\alpha_m}{2}\left\|\mathbf{U}^{(m)}\right\|_{\rm Fro}^2 +{\rm const.}\]
ただし、
\[
\mathbf{w}_d = \mathbf{u}_{i_1^{(d)}}^{(1)} \circ \mathbf{u}_{i_2^{(d)}}^{(2)} \circ \cdots \circ \mathbf{u}_{i_m^{(d)}}^{(m)}
\]
を近似の基準として用いています。対数尤度を用いることで、要素ごとに異なる近似の基準の比較が可能になり、自然に組み合わせることができます。

林さんはこの手法を上述のセンサーデータからの異常検知に応用して、複数人からなるグループの行動パターンの異常を検出することに成功したということです。

指数型分布族という抽象的な世界と、多種多様なセンサーデータからの高精度の異常検知という具体課題が密に繋がっているところが非常に面白いと感じました。

後半のお話は、カーネル法を用いたフルランクテンソルの穴埋め手法についてです。既存の行列分解やテンソル分解の手法は背後にあるデータの構造に何らかの“単純さ”（低ランク性）を仮定します。低ランクであるということは実質的に推定すべきパラメータは小さいということで、それによって少ないサンプルからでも構造を推定することができていました。しかし、実問題においては低ランク性の仮定は必ずしも成り立っているとは限りません。そこで林さんはカーネル法を使った、フルランク行列（およびテンソル）に対しても適応できる穴埋め方法を提案しました。

林さんのアイディアは、列間の類似度および行間の類似度を非線形な尺度（カーネル関数と呼びます）で算出し、それらを組み合わせることによって(i,j)番目の要素と(k,l)番目の要素の類似度を表現します。こうすることによって、機械学習でスタンダードなカーネル法と呼ばれる枠組みに沿って欠損データの類推が可能になります。行列・テンソル穴埋め問題においては要素数が多く、カーネル法を適用するには計算量が多くなってしまう傾向がありますが、今回のお話ではクロネッカー積の性質を用いることによって少ない計算量で済むとのことです。

この手法はさらに、与えられた行列（やテンソル）の要素だけでなく行や列に付随した付加情報も用いることができます。行列穴埋めは、例えば「誰（人）」が「何（アイテム）」を買ったというように人とアイテムの関係で構成される二次元配列を対象とします。この際、誰が何を買ったという事実だけでなく、その人がどのような人で買ったアイテムがどのような商品なのかという付加情報も使った方が、「ではその人が他に何を買いたがっているのか」ということを予測しやすくなります。 林さんの手法では、カーネル法の枠組みを用いることで、そのような付加情報を自然に盛り込むことができるそうです。

林さんの手法はmovielensという映画推薦システムの問題に適用され、mlcomp.orgという機械学習手法の性能を競いあうウェブページで現在も一位の性能を示しているそうです。（self-reflective-multi-task-GP-* というアルゴリズム)

テンソルという数理的な道具から出発し、実問題で高い性能を示す方法論へつながっている点が大変面白いと感じました。

数理6研助教 冨岡亮太 ＆ 数理5研助教 鈴木大慈

Generalization of Tensor Factorization and Applications

View more presentations from Kohei Hayashi

[1] Kohei Hayashi, Takashi Takenouchi, Tomohiro Shibata, Yuki Kamiya, Daishi Kato, Kazuo Kunieda, Keiji Yamada, and Kazushi Ikeda. Exponential family tensor factorization for missing-values prediction and anomaly detection. In the IEEE International Conference on Data Mining (ICDM'10), December 2010.

第１２回助教の会

第１２回数理助教の会では数理第４研究室ポスドクの坂下達哉さんに「量子i.i.d.状態の仮説検定問題における数値的手法の実装および計算精度に関する研究」というタイトルでおはなししていただきました。
坂下さんは昨年９月に電通大で学位を取得され、現在、さきがけ数学領域「統計モデル多様体の普遍的な性質のベイズ予測理論への応用」の研究員としても精力的に研究を進めています。



坂下さんは、ここ数十年で急速な発展を遂げた量子情報科学の分野で、特に、量子仮説検定の問題に対して、数値的な取り扱いを研究しています。 実験的に準備された量子状態が、２つの異なる量子状態のどちらであるかを、統計的仮説検定の問題として判定する方法を考えています。通常の仮説検定論が情報理論の主要な結果に応用されているように、量子仮説検定論は量子情報理論への応用を念頭においたものになっています。 坂下さんが取り組んでいる量子Hoeffdingの定理の問題設定は数学的に精密な定式化で煩雑なため、ここでは、Hoeffdingの定理のイメージを簡単に説明しておきます。

たとえば、1/2の確率で表が出るコインAと2/3の確率で表が出る偽コインBがあり、コインをn回ふって判断することにします。 コインを１０回ふって６回表が出たときだと、AなのかBなのか判断に迷います。 しかし、コインをふる回数を１００回、１０００回と増やしていくと、表の出る確率は1/2 もしくは2/3に近づいていき判断しやすくなります。 いいかえるとコインがAの時とBの時とで、それぞれ間違った判断をする確率（誤り確率）が十分小さくなります。 コインをふる回数nに対して誤り確率は指数的に減少していくことが知られており、その速さを指数誤り率と呼びます。さて、コインAをコインBに間違えてしまう確率とコインBをコインAに間違えてしまう確率の間にはトレードオフの関係があります。2つの指数誤り率のトレードオフはHoeffdingの定理によって簡単な形で表現できます。このような仮説検定の漸近理論の量子版が、坂下さんが注目している量子Hoeffdingの定理で、２００６年に証明されたばかりです。

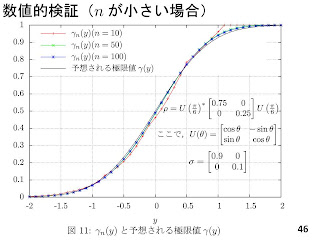
量子では試行回数ではなくテンソル積の次数nの極限を考え、指数誤り率は定理から簡明な形で書けますが、有限の場合には簡単にはかけません。 そこで、nが有限の場合の指数誤り率の振る舞いについて、数値的に詳しく調べたのが坂下さんの主要結果の一つです。


数値的に計算というと簡単そうに聞こえますが、この点について様々な工夫を行っています。本研究では、量子i.i.d.状態を表すテンソル積行列（指数サイズ）を多項式サイズの複数の行列に分解する「テンソル積の既約分解」という手法を用います。このような複数の行列に対して固有値計算が必要になるのですが、この計算で非常に大きな数値誤差が生じます。これは、このような行列では０の近くに固有値が密集しているためです。 この傾向は、nが大きくなるほど顕著になります。 実際、比較的小さなnでも、多倍長演算を用いて１００桁（10進法）程度で計算を行って、初めて有効な数値結果が得られています。計算機的にも非常にハードな計算ですので、 固有値ルーチンの改良、プロセス単位の並列化、そして、東大のスパコン（！）を用いてようやく可能になったそうです。数値計算の応用分野において、これほど大きな桁数を用いた固有値分解が必要な例は他になく、計算負荷を均等にする並列化法にも特色があり、数値解析や計算機実装の研究者にとっても面白いテーマを与えると思いました。



時間の関係で後半の一部は省略されましたが、最後に、新しい漸近理論に関する予想と数値的な検証について説明してもらいました。 既に示されている量子Hoeffdingの定理を用いて、数値計算が信頼できることを確認した後だからこそ検証に役に立つそうです。 数値的に試してうまくいくことを確認して、厳密な証明を与えるというのは、統計理論でもよくあるアプローチですが、 そこに量子論特有の難しさ（非可換な行列の扱いやテンソル積）が入っており、分野間融合の新しい可能性に溢れる話題だと思いました。

Sakashita

View more presentations from texja1234

数理第４研究室 助教 ＆さきがけ数学領域研究者（兼任）田中冬彦