第６回助教の会

第6回目となる今回の数理助教の会は，数理第2研究室の小林佑輔さんで，「点素パス問題に対するアルゴリズム」について発表していただきました．小林さんは組合わせ的問題に対するアルゴリズムの研究を行っていて，より具体的には，グラフ上の問題に対し，それを解くアルゴリズムの計算量の評価および高速化を考えています．こういった問題は，ちょっとした設定の違いでP（多項式時間で解ける）からNP困難に切り替わることがあり，このような問題の解きやすさの変化は大変魅力的であり，自身も興味をもって研究に取り組んでいるとのことです．



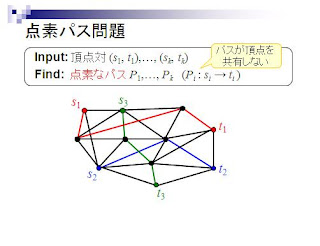
今回の発表では，表題のとおりグラフ上の点素パス問題について説明していただきました．点素パス問題とは，上図のように与えられた頂点対に対し，パスが頂点を共有しないようなパス（点素なパス）を見つける問題で，点素パス問題の研究の応用としては，VLSIの設計などが挙げられるそうです．一言で点素パス問題と言っても，グラフが無向グラフか有向グラフか，平面グラフかどうか、頂点対数kが定数か変数かなどの違いで，問題にはいくつかバリエーションが考えられ，それぞれの問題に対してそれを解くための理論的計算量（NP困難か多項式時間で解けるか線形時間で解けるか）が精力的に研究されています．単純なケースとして，頂点対の行き先tが一点である場合は，学部でも習うような最大流アルゴリズムにより多項式時間で解けますが，一般の入力に対しては，計算量の評価は難しいものになるとのことでした．

こういった研究の中で，今回はこの業界の大きな成果である，無向点素パス問題を多項式時間で解くRS(Robertson-Seymour)アルゴリズムについて簡単に紹介していただきました．このアルゴリズムは，まず扱っているグラフに対し木幅というグラフの複雑さの指標を計算し，木幅がある定数より小さければ動的計画法で解き，大きければ頂点を取り除いて木幅をどんどん小さくしていき，点素パスが見つかる（あるいはないことが分かる）までこの操作を繰り返すというもので，これは1980年代から現在に至る23本の論文にわたるグラフマイナー理論のもと完成したアルゴリズムだそうです（下図参照，赤枠のGraph Minors 13 にあるとのこと）．ただし，このRSアルゴリズムの計算量はグラフの頂点数nに対しては多項式時間であるものの，頂点対数kに依存する非常に大きな定数がかかるという問題点がありました．



これに対して小林さんは，オイラー的もしくは４辺連結なグラフを考え，この場合の辺素パス問題に対する単純なアルゴリズムを提唱し，これによりオーダー評価における頂点対数kに依存する係数がRSアルゴリズムに比べ非常に小さくなることを示しました．他にも，辺に長さが定義されているようなグラフに対する点素パス問題や，パス同士が隣り合う頂点対を持たないようなパスを見つける問題（誘導点素パス問題）といったものを扱い，それぞれに対して計算複雑度の評価を行っています．

実は僕はこの話を以前もっと短い時間で聞いていて，今回は２回目なのですが，知らない専門用語がたくさん登場するにもかかわらず最後まで楽しんで聞くことができました．そして２回目ですがBreak timeの点素パスは見つけられませんでした．どうも自分にこの手の研究は向いてないようですね．かなりセンスの必要な研究分野だろうなと改めて感じました．

数理第３研究室 助教 相島健助

Jokyo20110711

View more presentations from y-kobayashi.